Consistency and Replication
Back to ece454
Distribution:
- Partitioning
- Replication
Replication
Why?
- increase throughput
- e.g. Memcache, having multiple copies allows more things being served at once
- Lower latency
- Adds more hardware to the problem
- Greater fault tolerance
Examples
- GFS and HDFS
- Data storage and movement
- Map-reduce
- Math (speculative execution)
- MySQL server
- Data (shared mutable state)
- Very hard
Storage system behaviour
Sequential Consistency
This example is consistent:
| P1 |
w(x)a |
|
|
|
|
| P2 |
|
w(x)b |
|
|
|
| P3 |
|
|
r(x)b |
|
r(x)a |
| P4 |
|
|
|
r(x)b |
r(x)a |
If two writes occur in two different processes, they do not necessarily fall in temporal order. This only applies to writes in the same process.
There must be a sequential ordering of the events for it to be sequentially consistent.
This example is not:
| P1 |
w(x)a |
|
|
|
|
|
| P2 |
|
w(x)b |
|
|
|
|
| P3 |
|
|
r(x)b |
|
r(x)a |
|
| P4 |
|
|
|
r(x)a |
|
r(x)b |
Causal consistency
| P1 |
w(x)a |
|
|
w(x)c |
|
|
| P2 |
|
r(x)a |
w(x)b |
|
|
|
| P3 |
|
r(x)a |
|
|
r(x)c |
r(x)b |
| P4 |
|
r(x)a |
|
|
r(x)b |
r(x)c |
Has relationships "follows in program order" and "reads from", both examples of a causal precedence. This is causally consistent.
This is not:
| P1 |
w(x)a |
|
|
|
|
| P2 |
|
r(x)a |
w(x)b |
|
|
| P3 |
|
|
|
r(x)b |
r(x)a |
| P4 |
|
|
|
r(x)a |
r(x)b |
However, removing a read makes it consistent again:
| P1 |
w(x)a |
|
|
|
|
| P2 |
|
|
w(x)b |
|
|
| P3 |
|
|
|
r(x)b |
r(x)a |
| P4 |
|
|
|
r(x)a |
r(x)b |
Linearizability
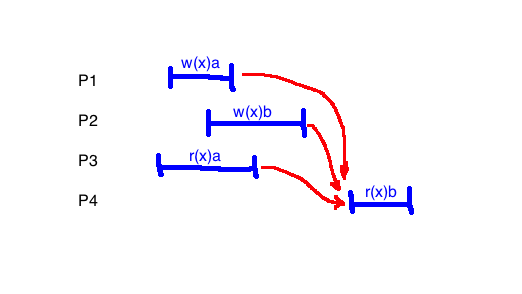
Arrows represent the happens before relation.
-
\(a\) happens before \(b\) if \(a.end \lt b.start\)
- Implicitly, each read happens after the most recent write
Potential orderings:
- O1: P2.w(x)b, P4.r(x)b, P2.w(x)a, P3.r(x)a
- Not ok since P1.w(x)a happens after P4.r(x)b
- O2: P1.w(x)a, P3.r(x)a, P2.w(x)b, P4.r(x)b
- ok: all read values make sense, no backwards arrows
Since there is a valid total order, the example is linearizable.
Alternative interpretation
- Place a dot representing a single instant where the event happens, where the dot has to be between the start and end of the operation
- Connect dots so that you never go backwards and read values make sense
- If this is possible, it is linearizable
This example is not linearizable:
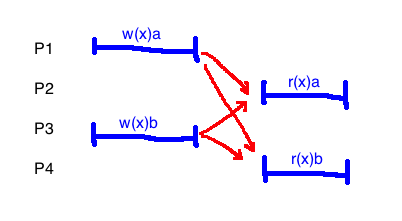
- Any way that we find a total order, both writes must come before both reads
- It is not possible to do this and have the reads make sense
Linearizability check algorithm
- Make a graph where the vertices are each operation
- Add an edge \((a, b)\) if:
- \(a.end \lt b.start\)
- there is a read after \(b\) that reads the value \(b\) wrote, and \(a\) wrote a different value
- If there is a cycle in this graph, it is not linearizable
Another:
- Make a graph where the vertices are the values of the thing being read/written to
- Add an edge from \(a, b\) if there is a write of \(b\) after a read of \(a\)
- Check for cycles
Eventual consistency
- If no updates take place for a long time, all replicas will gradually become consistent.
- In the absence of new writes from clients, all servers will eventually hold the same data.
This allows different processes to observe write operations taking effect in different orders, even when these write operations are related by "causally precedes" or "happens before"
e.g. This does not have eventual consistency
- P1.w(x)a
- P2.w(x)b
- P3.r(x)a
- P4.r(x)b
- Repeat steps 3 and 4 forever.
Properties
- There are all examples of safety properties
- Sequential consistency is a subset of causal consistency (it is a stronger definition)
- Linearizability is a subset of sequential consistency
- linearizable \(\Rightarrow\) sequentially consistent \(\Rightarrow\) causally consistent
Guarantees: Monotonicity
Every time you do a read, it should either be the same value as before, or a newer version
Negative example:
| P1 |
w(x)a |
|
|
| P2 |
w(x)b |
|
|
| P3 |
|
r(x)a |
r(x)b |
| P4 |
|
r(x)b |
r(x)a |
Positive example:
| P1 |
w(x)a |
|
|
|
|
| P2 |
w(x)b |
|
|
|
|
| P3 |
|
r(x)a |
r(x)b |
|
|
| P4 |
|
|
|
r(x)b |
r(x)a |
Guarantees: Read your own writes
If you write a value and then do a read, you should get the value you just wrote, not an older one
Protocols
Primary backup
A server has the true copy
Quorum
There is a maximum number of servers \(f\) that are allowed to fail, and a value is considered written after a majority have written.
Let \(N\), \(N_R\), and \(N_W\) be total number of replicas for a data object \(x\), the size of the read quorum, and the size of the write quorum.
In distributed databases, RW quorums must satisfy:
-
\(N_R + N_W \gt N\) (read and write quorums overlap)
-
\(N_W + N_W \gt N\) (two write quorums overlap)
Partial quorums
Partial quorums lack overlap
-
\(N_R + N_W \gt N\) (strong consistency)
-
\(N_R + N_W \le N\) (weak consistency)
Use last-timestamp-wins to deal with conflicts
Fault Tolerance
Dependability
- Availability (e.g. 99.99...%)
- Reliability
- Safety
- Maintainability
Fault types
- Transient: goes away on its own
- Intermittent: fault that happens only some of the time, often related to electrical contacts
- Permanent: much easier to diagnose
Masking failures
- Have redundant, identical processes
- Arranged in a flat group: all have equal weight
- Arranged hierarchically: has a leader/coordinator
- How many backups?
- If you need to tolerate \(f\) failures, you need at least \(2f+1\) processes to be able to have a majority
- If you have primary backups, you need \(f+1\), but with the assumption that you will fix the broken ones soon
Consensus Problem
- Has interfaces
propose(x), decide()
- Each process calls
propose() at most once, and decide() at most once
- Safety properties
- Agreement: two calls to
decide() never return different values
- Validity: If
decide() returns v, then some process called propose(v)
- Liveness/Termination policy: calls to
propose(x) and decide() eventually terminate
Zookeeper
Coordination
- group membership
- leader election
- dynamic configuration
- status monitoring
- queueing
- barriers
- critical sections
- sequentially consistent writes
- serializable reads (may be stale)
- client FIFO ordering
Events
- clients request change notifications
- service does timely notifications
- do not block write requests
- clients get notification of a change before they see the result of a change
Znodes
- Can be ephemeral
- Can be sequence (used for symmetry breaking)
Fault-tolerant RPCs
Semantics under failures:
- client is unable to locate the server
- request message from the client to server is lost
- server crashes after receiving a request
- reply message from server to client is lost
- client crashes after sending a request
Primary backup
Update:
- Client sends to primary
- Primary locks exclusive lock
- Primary sends to backup
- Backup sends acknowledgement to primary
- Primary unlocks
- Primary sends an acknowledgement to client
Read:
- client sends to primary
- Primary locks shared lock
- Primary gets data
- Primary unlocks
- Primary sends data to client
Quorum (ACID)
- Client to server to send data and acquire locks
- Server sends data to client
- Client to server to release locks
- Server sends acknowledgement
To get linearizability:
- For read quorum, we want \(N_R + N_w \gt N\)
- For write quorum, \(N_W + N_R \gt N\)
Quorum (NoSQL key-value store)
- No locking
- Operations have timestamps, which are used to break ties (look at the fresher timestamp)
Anti Entropy
Entropy is when servers have different values for the same key.
Solution: use a Merkle tree, hashing the hashes of its child node values
Checkpoints
2-phase commit is the A in ACID. 2-phase locking is the I in ACID.
A distributed checkpoint is a collection of checkpoints (one per process).
- If receive event of some message \(m\) is recorded, then the send for \(m\) is also recorded.
The recovery line is the most recent distributed snapshot.
Coordinated checkpointing algorithm
- Phase 1
- Coordinator sends
CHECKPOINT_REQUEST
- Upon receiving the above message:
- Pause processing incoming messages
- Take local checkpoint
- Return ack to coordinator
- Phase 2
- Coordinator waits for all processes to send ack
- Coordinator sends
CHECKPOINT_DONE to all processes
- Upon receiving the above message, processes resume processing messages


